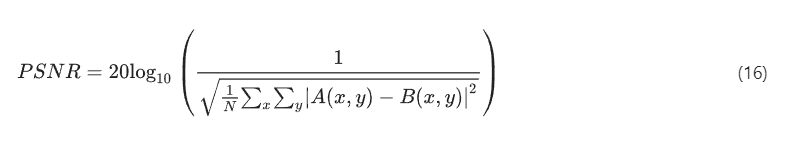All-optical complex field imaging using diffractive processors
Jingxi Li, Yuhang Li, Tianyi Gan, Che-Yung Shen, Mona Jarrahi & Aydogan Ozcan
Complex field imaging, which captures both the amplitude and phase information of input optical fields or objects, can offer rich structural insights into samples, such as their absorption and refractive index distributions. However, conventional image sensors are intensity-based and inherently lack the capability to directly measure the phase distribution of a field. This limitation can be overcome using interferometric or holographic methods, often supplemented by iterative phase retrieval algorithms, leading to a considerable increase in hardware complexity and computational demand. Here, we present a complex field imager design that enables snapshot imaging of both the amplitude and quantitative phase information of input fields using an intensity-based sensor array without any digital processing. Our design utilizes successive deep learning-optimized diffractive surfaces that are structured to collectively modulate the input complex field, forming two independent imaging channels that perform amplitude-to-amplitude and phase-to-intensity transformations between the input and output planes within a compact optical design, axially spanning ~100 wavelengths. The intensity distributions of the output fields at these two channels on the sensor plane directly correspond to the amplitude and quantitative phase profiles of the input complex field, eliminating the need for any digital image reconstruction algorithms. We experimentally validated the efficacy of our complex field diffractive imager designs through 3D-printed prototypes operating at the terahertz spectrum, with the output amplitude and phase channel images closely aligning with our numerical simulations. We envision that this complex field imager will have various applications in security, biomedical imaging, sensing and material science, among others.
Introduction
Optical imaging can characterize diverse properties of light, including amplitude, phase, wavelength, and polarization, which provides abundant information about samples, such as their morphology and composition. However, conventional image sensors and focal plane arrays, based on e.g., Complementary Metal-Oxide-Semiconductor (CMOS) or Charge-Coupled Device (CCD) technologies, are inherently constrained to detecting only the intensity of the optical field impinging on their active area. Measuring the phase information of a complex field presents challenges, which require indirect encoding through interferometric or holographic detection systems1,2,3. Some of the traditional examples of phase imaging techniques include Zernike phase contrast microscopy and interferometric microscopy. Remarkedly, interferometry-based techniques4,5,6 exhibit very high accuracy in phase measurements (exceeding 1/100 of a wavelength) and allow one to directly obtain wavefront aberrations at very large apertures; however, the relative complexity of decoding interferograms and the sensitivity of the measurement equipment to vibrations hinder their wide applications. Subsequent developments in quantitative phase imaging (QPI) have enabled high-precision characterization of phase information; advances such as the Fourier phase microscopy7, Hilbert phase microscopy8 and digital holographic microscopy9,10,11,12,13,14,15 have also emerged, making QPI a potent label-free optical measurement technique. Nevertheless, these QPI methods often necessitate relatively bulky experimental setups and rely on iterative algorithms based on multiple measurements to digitally reconstruct the desired phase information, leading to slow imaging speeds. In parallel, Shack-Hartmann sensors16,17 can provide phase information by analyzing wavefront distortions inferred from the displacement of light spots created by a perforated mask. This approach, while eliminating the need for a reference wavefront or field, faces challenges in detection resolution due to its discrete measurement nature and still demands data processing for precise phase or wavefront reconstructions. In addition to these, there are other methods that decompose the wavefront into discrete elements, such as Zernike polynomials, offering a direct path to understanding aberrations in wavefronts exhibiting small phase variations18,19,20,21. However, these approaches are less suitable for investigating phase objects with complex structures and high spatial frequencies, underscoring a limitation in their broad applicability.
Recently, fueled by the advances made in deep learning, the application of deep neural networks has been adopted for accurate and rapid reconstruction of phase information in complex fields through a single feed-forward operation22,23,24,25,26,27,28,29. While these deep learning-based approaches offer considerable benefits, they typically demand intensive computational resources for network inference, requiring the use of graphics processing units (GPUs). Simultaneously, the progress in micro- and nano-fabrication technologies has facilitated the development of metasurfaces30,31,32,33,34,35,36,37,38 and thin-film optical components39,40 for QPI applications. However, the functionality of these devices still relies on indirect encoding processes that generate intensity variations on the sensor plane, such as diffused speckles30 or polarized interference patterns38. These existing solutions, therefore, necessitate digital computation for image reconstruction and, in certain cases, also require the incorporation of additional hardware along the optical path, such as polarizers and polarization cameras.
In this work, we demonstrate the design of a complex field imager that can directly capture the amplitude and phase distributions of an incoming field using an intensity-only image sensor array. As shown in Fig. 1a, this complex field imager is composed of a series of spatially engineered diffractive surfaces (layers), which are jointly optimized using supervised deep learning algorithms to successively perform the modulation of incoming complex fields. This diffractive architecture, known as a diffractive optical neural network, has previously been explored for all-optical information processing covering various applications, including all-optical image classification41,42, space-to-spectrum encoding42,43, logic operations44,45,46, optical phase conjugation47, among others48,49,50,51,52,53,54,55,56,57,58,59,60. Within the architecture of our diffractive complex field imager, the diffractive surfaces are trained to simultaneously perform two tasks: (1) an amplitude-to-amplitude (A → A) transformation and (2) a phase-to-intensity (P → I) transformation. Here, the first task involves mapping the amplitude of the incoming complex field to a specific output field of view (FOV) that is solely dedicated to amplitude imaging, independent of the input wave’s phase profile. The second task, on the other hand, aims to approximate a nonlinear transformation by converting the phase of the incoming wave into an intensity pattern at another output FOV, exclusively used for quantitative phase imaging, QPI. Therefore, by placing complex objects or feeding complex fields into the input FOV of the diffractive complex field imager and measuring the intensity distributions at its output FOVs, the amplitude and phase information of the input complex objects/fields can be directly obtained within a single intensity-only image recording step, eliminating the necessity for any form of image reconstruction algorithms. In addition to this spatially multiplexed design of the diffractive complex field imager, termed design I (Fig. 1a), we also explored additional complex field imager designs by incorporating wavelength multiplexing. As illustrated in Fig. 1b, c, these wavelength multiplexed designs, termed designs II and III, operate by detecting the output amplitude and phase signals at two distinct wavelengths ( and , respectively). The difference between designs II and III is that design II utilizes a shared FOV for both the amplitude and phase channel outputs, while design III maintains two spatially separated FOVs, each dedicated to either the output amplitude or phase images.
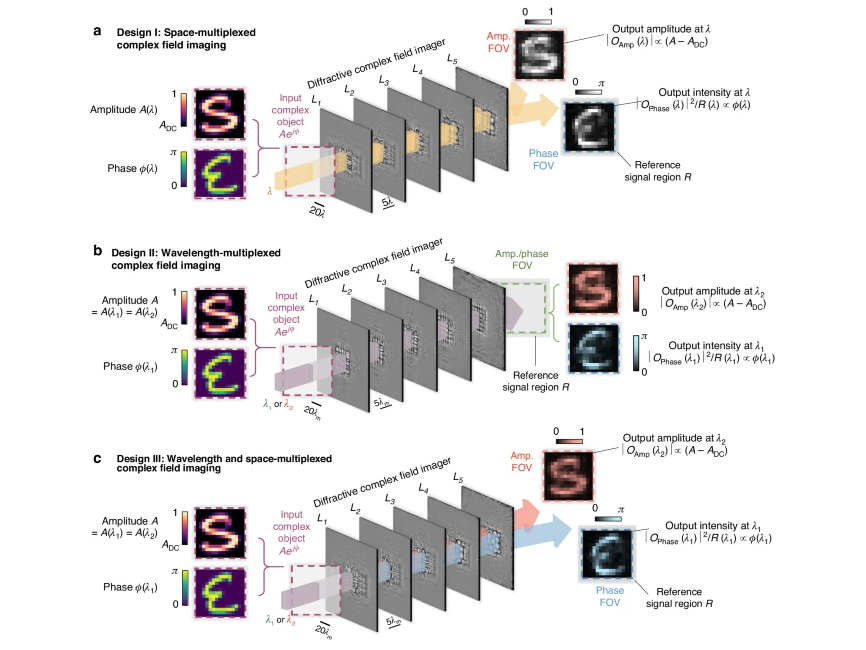
Schematics for different designs of our diffractive complex field imager. a Illustration showing a spatially multiplexed design for the diffractive complex field imager (design I), which performs imaging of the amplitude and phase distributions of the input complex object simultaneously by channeling the output amplitude and phase images onto two spatially separate FOVs at the output plane, i.e., the amplitude and phase FOVs (or FOVAmp and FOVPhase). b Illustration for an alternative design of the diffractive complex field imager using wavelength multiplexing (design II), wherein the output amplitude and phase profiles are directly measured using a common output FOV but at different wavelengths, i.e., and , respectively. c, Illustration for design III of the diffractive complex field imager, wherein the output amplitude and phase images are measured using two spatially separate FOVs (FOVAmp and FOVPhase) and also at different wavelengths ( and , respectively)
After completing the training of these different designs, we blindly tested the performance and generalization capabilities of our trained diffractive complex field imager models. We quantified their imaging errors using thousands of examples of input complex fields, each composed of independent information channels encoded in the amplitude and phase of the input field. The results demonstrated that our diffractive models could successfully generalize to new, unseen complex test fields, including those with structural features distinctly different from the training objects. Through numerical simulations, we further analyzed the spatial resolution and sensitivity of both the amplitude and phase channels of our diffractive complex field imagers. These analyses revealed that our designs could resolve amplitude features with a linewidth of ≥1.5 and phase features with a linewidth of ≥3 , where represents the mean wavelength. Furthermore, our studies showed that by integrating an additional diffraction efficiency-related loss term into the training function, one could achieve diffractive imager models with enhanced output power efficiencies with minimal compromise in imaging performance.
Apart from these numerical analyses, we also conducted an experimental proof-of-concept demonstration of our diffractive complex field imagers using the terahertz part of the spectrum by fabricating the resulting diffractive layers using 3D printing. For our experiments, we constructed test objects (never seen during the training) with spatially structured amplitude or phase distributions through 3D printing and surface coating techniques. Our experimental results successfully reconstructed the amplitude and phase images of the test objects, closely matching our numerical simulations and the ground truth, validating the effectiveness of our diffractive complex field imager designs. While our experimental demonstrations were conducted in the terahertz spectrum, our designs are scalable and can be adapted to other spectral bands by scaling their dimensions proportional to the wavelength of operation. The compact size of our diffractive designs, with an axial span of ~100 × , facilitates easy integration into existing optical imaging systems and focal plane arrays that operate at different parts of the electromagnetic spectrum, including the visible spectrum. For operation within the visible band, our design can be physically implemented through various nano- and microfabrication techniques, such as two-photon polymerization-based nanolithography50,61. Furthermore, this complex field imager design also does not include any components that are sensitive to the polarization of light, maintaining its amplitude and phase imaging function regardless of the input polarization distribution of the input field. Given all these advantages, including the small footprint, speed of all-optical computation and low-power operation, we believe that this all-optical complex field imaging approach will find broad applications in e.g., defense/security, biomedical imaging, sensing and material science.
Materials

Pr Series
Results
Designs of diffractive complex field imagers
Figure 1a illustrates a spatially multiplexed design of our diffractive complex field imager, termed the design I. This diffractive imager is composed of 5 diffractive layers (i.e., L1, L2, …, L5), where each of these layers is spatially coded with 200 × 200 diffractive features, with a lateral dimension of approximately half of the illumination wavelength, i.e., ~ /2. These diffractive layers are positioned in a cascaded manner along the optical axis, resulting in a total axial length of 150 for the entire design. A complex input object, , illuminated at is placed at the input plane in front of the diffractive layers. This complex object field exhibits an amplitude distribution that has a value range of [ADC, 1], along with a phase distribution ranging within [0, απ]. Here, ADC denotes the minimum amplitude value of the input complex field, and α is the phase contrast parameter of the input complex field. Without loss of generality, we selected default values of ADC and α as 0.2 and 1, respectively, for our numerical demonstrations. Note that it’s essential to work with ADC ≠ 0 since otherwise the phase would become undefined. After the input complex fields are collectively modulated by these diffractive layers L1-L5, the resulting optical fields at the output plane are measured by the detectors within two spatially separated output FOVs, i.e., FOVPhase and FOVAmp, which produce intensity distributions and that correspond to the phase and amplitude patterns of each input complex field, respectively. In addition, we also defined a reference signal region at the periphery of the FOVPhase, wherein the average measured intensity across is used as the reference signal for normalizing the quantitative phase signal . This normalization process is essential to ensure that the detected phase information is independent of the input light intensity fluctuations, yielding a quantitative phase image , regardless of the diffracted output power. Overall, the objective of our training process is to have the phase image channel output approximate the ground truth phase distribution of the input complex field, i.e., , demonstrating an effective phase-to-intensity (P → I) transformation. Concurrently, the training of the diffractive layers also aims to have the diffractive output image in the amplitude channel, i.e., , proportionally match the ground truth amplitude distribution of the input complex field after subtracting the amplitude DC component ADC, i.e., , thereby achieving a successful amplitude-to-amplitude (A → A) transformation performed by the diffractive processor. Note that phase-to-intensity transformation is inherently a nonlinear function58. In the phase imaging channel of our diffractive complex-field imager, the amplitude-squared operation as part of the intensity measurement at the sensor plane represents the only occurrence of nonlinearity within the processing pipeline.
In addition to the spatially multiplexed design I described above, we also created an alternative complex field imager design named design II by incorporating wavelength multiplexing to construct the amplitude and phase imaging channels. As illustrated in Fig. 1b, this approach utilizes a dual-color scheme, where the amplitude and phase of the input images are captured separately at two distinct wavelengths, with dedicated to the phase imaging channel and dedicated to the amplitude imaging channel. As an empirical parameter, without loss of generality, we selected = × 1.28 and + = 2 for our numerical diffractive designs. With this wavelength multiplexing strategy in design II, the amplitude and phase imaging FOVs can be combined into a single FOV – as opposed to 2 spatially separated FOVs as employed by design I shown in Fig. 1a. Consequently, the output amplitude and phase images, i.e., and , can be recorded by the same group of sensor pixels.
As illustrated in Fig. 1c, we also developed an additional complex field imager design, referred to as design III, which integrates both space and wavelength multiplexing strategies in constructing the amplitude and phase imaging channels. Specifically, design III incorporates two FOVs that are spatially separated at the output plane (similar to design I) for amplitude and phase imaging, also utilizing two different wavelength channels (akin to design II) to encode the output amplitude/phase images separately.
Following these design configurations (I, II and III) depicted above, we performed their numerical modeling and conducted the training of our diffractive imager models. For this training, we constructed an image dataset comprising 55,000 images of EMNIST handwritten English capital letters, and within each training epoch, we randomly grouped these images in pairs – one representing the amplitude image and another representing the phase image – thereby forming 27,500 training input complex fields. The phase contrast parameter αtr used for constructing these training input complex fields was set as 1. We utilized deep learning-based optimization with stochastic gradient descent to optimize the thickness values of the diffractive features on the diffractive layers. This training was targeted at minimizing a custom-designed loss function defined by the mean squared error (MSE) between the diffractive imager output amplitude and phase images with respect to their corresponding ground truth. More information about the structural parameters of the diffractive complex field imagers, the specific loss functions employed, and additional aspects of the training methodology can be found in the Methods section.
Numerical results and quantitative performance analysis of diffractive complex field imagers
After the training phase, the resulting diffractive layers of our complex field imager models following designs I, II and III are visualized in Supplementary Figs. S1a, S2a and Fig. 2a, respectively, showing their thickness value distributions. To evaluate and quantitatively compare the complex field imaging performances of these diffractive processors, we first conducted blind testing by selecting 10,000 test images from the EMNIST handwritten letter dataset that were never used in the training set and randomly grouped them in pairs to synthesize 5000 complex test objects. To compare the structural fidelity of the resulting output amplitude and phase images (i.e., and ) produced by our diffractive complex field imager models, we quantified the peak signal-to-noise ratio (PSNR) metrics between these diffractive output images and their corresponding ground truth (i.e., and ). Our results revealed that, for the diffractive imager model using design I that performs space-multiplexed complex field imaging, the amplitude and phase imaging channels provided PSNR values of 16.47 ± 0.96 and 14.90 ± 1.60, respectively, demonstrating a decent imaging performance. Additionally, for the diffractive imager models using designs II (and III), these performance metrics became 16.46 ± 1.02 and 14.98 ± 1.51 (17.04 ± 1.06 and 15.06 ± 1.63), respectively. Therefore, design III demonstrated a notable performance advantage over the other two models in both phase and amplitude imaging channels when both the space and wavelength multiplexing strategies were used. Apart from these quantitative results, we also presented exemplary diffractive output images for the three models of designs I, II and III in Supplementary Figs. S1b, S2b and Fig. 2b, respectively. These visualization results clearly show that our diffractive output images in both amplitude and phase channels present structural similarity to their input ground truth, even though these input complex fields were never seen by our diffractive models before. These analyses demonstrate the internal generalization of our diffractive complex field imagers, indicating their capability to process new complex fields that have similar statistical distributions to the training dataset.

Blind testing results of the diffractive complex field imager using design III. a Thickness profile of the trained layers of the diffractive complex field imager following the design III in Fig. 1c. The layout of the amplitude and phase FOVs in comparison to the size of a diffractive layer is also provided. b Exemplary blind testing input complex objects never seen by the diffractive imager model during its training, along with their corresponding output amplitude and phase images. c, d Same as b, except that the testing images are taken from the MNIST and QuickDraw datasets, respectively, demonstrating external generalization to image datasets with different structural distributions
We also conducted blind testing of these diffractive complex field imager designs by synthesizing input fields from other datasets where the complex images exhibit distinctly different morphological features compared to the training complex field images. For this purpose, we selected the MNIST handwritten digits62 and the QuickDraw image63 datasets, and for each dataset, we synthesized 5000 input complex fields to test our diffractive models blindly. When using the MNIST-based complex field images, the amplitude and phase PSNR values of our diffractive complex field imager models using designs I, II and III were quantified as (16.59 ± 0.71, 15.42 ± 1.28), (16.40 ± 0.68, 15.53 ± 1.25) and (17.05 ± 0.78, 15.59 ± 1.32), respectively. The corresponding diffractive output images for these results are also exemplified in Supplementary Figs. S1c, S2c and Fig. 2c. When testing using input complex fields synthesized from the QuickDraw images, these PSNR values revealed (14.42 ± 0.94, 13.34 ± 1.10), (14.17 ± 1.01, 13.54 ± 1.61) and (14.72 ± 0.97, 13.46 ± 1.13), with exemplary diffractive output images visualized in Supplementary Figs. S1d, S2d and Fig. 2d, respectively. Once again, these PSNR values, along with the visualization results of the output patterns, demonstrate that all our diffractive models (following designs I, II and III) achieved successful reconstructions of the amplitude and phase channel information of the input complex fields, wherein the design III model presented slightly improved performance over the other two designs. Importantly, these analyses demonstrate the external generalization capabilities of our diffractive imagers, positioning them as general-purpose complex field imagers that can handle input complex field distributions markedly distinct from those encountered during their training stage.
Next, we quantified the complex field imaging performance of our diffractive models as a function of the phase contrast and spatial resolution of the incoming complex fields. For this analysis, we selected various grating patterns to form our test images, which have different linewidths and are oriented in either horizontal or vertical directions. We first considered using these grating patterns encoded within either the phase or the amplitude channels of the input complex fields, forming phase-only or amplitude-only grating test objects. To be more specific, the phase-only input fields were set to have a uniform distribution within their amplitude channel, while the amplitude-only input fields were set to have their phase channel values set as zero/constant. For both kinds of gratings, we selected their linewidths as 1.5 or 3 to generate the grating patterns, and tested the spatial resolution for the amplitude and phase imaging channels using our diffractive models; here = for the design I model and = ( + )/2 for the designs II and III. For phase-only gratings with linewidths of 3 , we also used different phase contrast parameters {0.25, 0.5, 1} to form grating patterns with different phase contrast so that we can evaluate the sensitivity of phase imaging by our diffractive complex field processors. To better quantify the performance of our diffractive complex field imagers for these test grating patterns, we used a grating image contrast (Q) as our evaluation metric, defined as:

The results of using these amplitude- or phase-only grating patterns as input fields to our diffractive models using designs I, II and III are provided in Supplementary Figs. S3a, b, S4a, b and Fig. 3a, b, respectively. Through visual inspection and quantification of grating image contrast Q values, our diffractive imager models were found to resolve most of the amplitude-only grating objects of different linewidths and orientations, with quantified Q values consistently above 0.17. The only exception is that the diffractive model using design II fell short in resolving the horizontal grating patterns with 1.5 linewidth, achieving Q < 0.1. For the phase-only grating inputs, all three diffractive models succeeded in resolving the gratings with {0.5, 1} and linewidths of 3 , presenting Q values consistently over 0.19. However, when using the phase-only grating inputs with 0.25 and linewidths of 3 or those with 1 and linewidths of 1.5 , all of our diffractive models struggle to provide consistently clear grating images, exhibiting relatively poor Q values of ≤0.1. These findings reveal that our diffractive imager models exhibit similar performance in imaging resolution and phase sensitivity, providing an amplitude imaging resolution of >1.5 for amplitude-only objects and a phase imaging resolution of ≥3 for phase-only objects with ≥ 0.5. We also calculated the average Q values for different diffractive models using these amplitude- or phase-only grating inputs; the design III model emerges as the most competitive one, presenting average Q values of 0.418 and 0.181 for the amplitude and phase channels, respectively. The suboptimal performance of the design II model, we believe, can primarily be attributed to its utilization of the same output FOV for both the phase and amplitude image formation. This strategy results in the overlap of the diffractive features to serve the two imaging channels, thereby not fully utilizing the degrees of freedom provided by the diffractive layers. This is also corroborated by the visualization of the diffractive layer designs shown in Supplementary Fig. S2a: compared to designs I and III, the areas with significant modulation patterns in the design II layers are significantly smaller and more concentrated in the central region, indicating a less efficient utilization of the diffractive degrees of freedom available for optimization, consequently limiting its imaging performance.

Performance analysis of the diffractive complex field imager model shown in Fig. 2. a Imaging results using phase-only gratings as input fields. The binary phase grating patterns encoded within the phase channel of the input objects are shown and compared with the resulting output amplitude and phase images produced by our diffractive imager (i.e., and ). For each diffractive output image, the grating image contrast Q and SCR values were quantified and shown in red and blue numbers, respectively. b Same as in a, except that the amplitude-only gratings are used as input fields. c Imaging results using complex grating objects as input fields. These grating test objects include ones with the same grating patterns encoded in both the amplitude and phase channels (top), as well as ones where horizontal and vertical gratings are orthogonally placed, with one encoded in the phase channel of the input field and the other encoded in the amplitude channel (bottom)
n addition to the analyses of spatial resolution and phase sensitivity, we also utilized amplitude- and phase-only grating images to investigate the crosstalk between the amplitude and phase imaging channels of our diffractive complex field imagers. Since the amplitude-only grating inputs have constant/zero phase distributions, the ground truth of their corresponding diffractive output images in the phase channel should have zero intensities, where the residual represents the crosstalk coming from the amplitude channel. Similarly, for the phase-only grating inputs that have a uniform amplitude distribution (ADC), their diffractive output images in the amplitude channel should reveal no intensity distributions, with the residual representing the crosstalk coming from the phase channel. As shown by the diffractive output images in Supplementary Figs. S3a, b, S4a, b and Fig. 3a, b, we observe some crosstalk components in the amplitude and phase channel imaging results. To provide a quantitative evaluation of this crosstalk, we used the signal-to-crosstalk ratio (SCR) metric, defined as:

where and denote the resulting output phase image when encoding the same grating pattern within the phase and amplitude channels of the input complex field, respectively; the first term represents the true signal, and the latter represents the crosstalk term in Eq. (2). Similarly, and denote the resulting output amplitude image when encoding the same grating pattern within the amplitude and phase channels of the input complex field, respectively. denotes the intensity summation operation across all the pixels. Following these definitions, we quantified the and values for all the grating imaging outputs in Supplementary Figs. S3a, b, S4a, b and Fig. 3a, b. These SCR analyses reveal that, for all the diffractive imager models, the grating inputs with 1.5 linewidth and 1 present a ~30% lower and a ~53% lower when compared to their counterparts with 3 linewidth, revealing that imaging of finer, higher-resolution patterns is more susceptible to crosstalk. Furthermore, we found that an increase in the input phase contrast ( leads to more crosstalk in the output amplitude channel, which results in a lower value; for example, from >3.5 for 0.25 down to 2.5-3 for 1. Additionally, we calculated the average and values across these grating images for different diffractive imager models; for the diffractive models using designs I, II and III, the average values are 2.805, 3.178 and 3.155, respectively, and the average values are 2.331, 2.262 and 2.252, respectively.
These analyses were performed based on amplitude and phase-only grating objects. Beyond that, we also used complex-valued gratings to further inspect the imaging performance of our diffractive models. Specifically, we created complex test fields that have the same grating patterns encoded in both the amplitude and phase channels. The results reported in the top row of the Supplementary Figs. S3c, S4c and Fig. 3c revealed that all our diffractive imager models are capable of distinctly resolving complex gratings with 3 linewidth, while being largely able to resolve those with 1.5 linewidth, albeit with occasional failure. We further created complex fields by orthogonally placing horizontal and vertical gratings, with one of these gratings encoded in the phase channel of the input field and the other encoded in the amplitude channel. As evidenced by the bottom row of Supplementary Figs. S3c, S4c and Fig. 3c, our diffractive models could successfully reconstruct the amplitude and phase patterns of the input complex fields with a grating linewidth of 3 .
Impact of input phase contrast on the performance of diffractive complex field imagers
In the analyses conducted so far, all the input fields fed into our diffractive model maintained a consistent phase contrast with an value of 1, i.e., , regardless of the training and testing phases. Next, we investigated the impact of greater input phase contrast on the performance of diffractive complex field imagers. For this analysis, we utilized the same diffractive design III model shown in Fig. 2 and tested its imaging performance using the same set of complex test objects used in Fig. 2b, but with an increased object phase contrast, , chosen within a range between 1 and 1.999 (i.e., ∈ [0, 2π)). The corresponding results are shown as the blue curve in Fig. 4a, illustrating a degradation in the imaging performance of the diffractive model as increases. This degradation is relatively minor in the PSNR results for the amplitude channel but more pronounced for the phase channel. Specifically, as increases from 1 to 1.5, the average amplitude PSNR value slightly drops from 17.04 to 15.82, while the phase PSNR falls from 15.06 to 11.96. When approaches 2, the average amplitude and phase PSNR values further decrease to 15.34 and 9.87, respectively. The visual examples in Fig. 4b and Supplementary Fig. S5a, which correspond to the cases of = 1.5 and 1.25, respectively, reveal that the amplitude channel of the diffractive model can consistently resolve the amplitude patterns of the objects, which were never encountered during the training phase. However, in the phase channel, despite the patterns being distinguishable and very well matching the ground truth, their intensities were lower than the correct level, leading to incorrect quantitative phase values and, thus, a drop in the phase PSNR values.
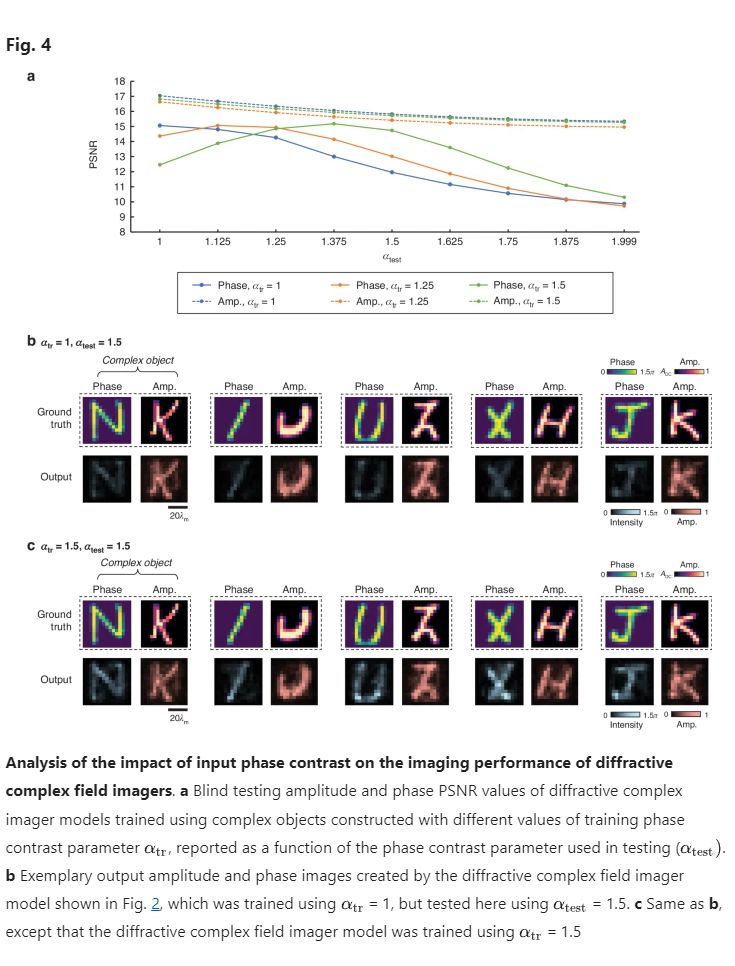
To address this limitation, we explored training two additional diffractive models using higher phase contrast values of 1.25 and 1.5, respectively. The quantitative evaluation results for these models are presented in Fig. 4a as orange and green curves, respectively. The findings indicate that, compared to the original model trained with = 1, the diffractive model employing = 1.5 exhibits a significantly enhanced imaging performance in the phase channel for > 1.25. For instance, at = 1.5, the phase PSNR improved from 11.96 to 14.42, while the amplitude PSNR remained almost identical across various values. A similar improvement was also observed with the other diffractive model trained using = 1.25. These findings are further confirmed by the exemplary visualization results shown in Fig. 4c and Supplementary Fig. S5b; the quantitative phase signals in the phase channel of these new diffractive models markedly ameliorate the issues encountered by the original model. Nonetheless, it is also noted that these new models exhibited some minor disadvantages; for example, the diffractive model trained using = 1.5 demonstrated slightly inferior phase PSNR results at < 1.25 compared to the original model. This suggests a propensity of our diffractive imager models to achieve better imaging performance on complex test objects with phase dynamic ranges akin to those encountered during the training.
It is also important to note that the current design of our diffractive complex field imager is specifically tailored for imaging thin complex objects. For such thin objects, their phase variations are relatively slower. In contrast, substantially thicker objects can exhibit rapidly varying phase distributions, leading to phase wrapping issues. These complexities would pose a challenge for the diffractive network-based complex field imager to perform effective processing and image formation. To potentially address this challenge, incorporating a wavelength-multiplexing strategy (similar to that used in certain QPI methods) into the diffractive imager framework could be a potential path forward. Such an approach, which is left as future work, may involve leveraging the diffractive network for all-optical processing across multiple wavelength channels, followed by minimal digital post-processing to accurately reconstruct quantitative phase signals from wrapped phase information acquired at different wavelengths.
Output power efficiency of diffractive complex field imagers
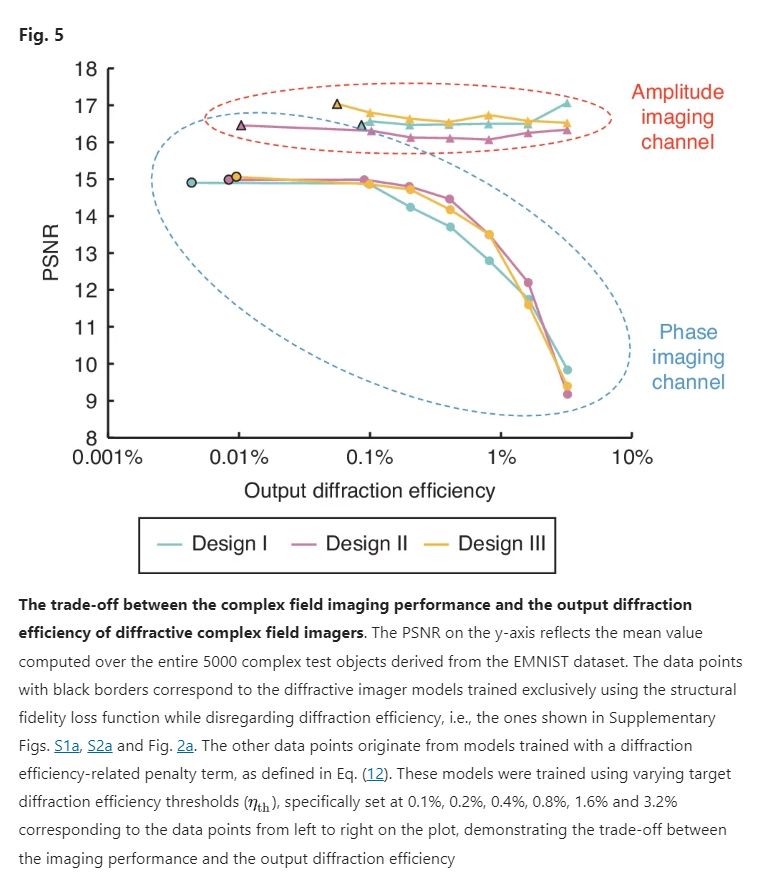
To quantify the output diffraction efficiencies of our complex field imagers, we utilized 5000 test complex fields created from the EMNIST image dataset, and calculated the average diffraction efficiencies of our diffractive complex field imager models. By integrating an additional loss term into our training loss function to balance the complex field imaging performance along with the output diffraction efficiency, we demonstrated the feasibility of increased power efficiency for all three designs (I, II and III), with minimal compromise in the output image quality. The added loss term, denoted as , is specifically designed to control and improve the output diffraction power efficiency, with its definition given by:
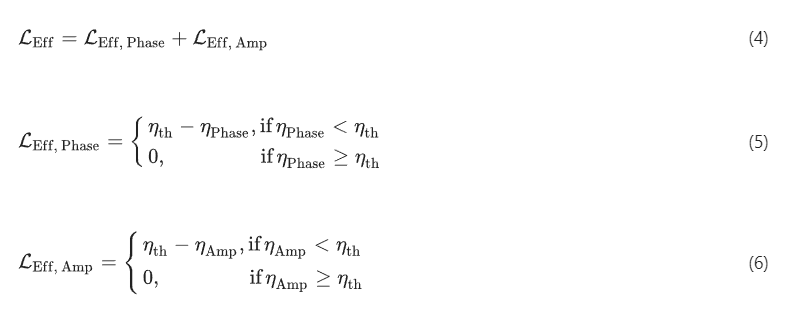
where and denote the output diffraction power efficiency within FOVPhase and FOVAmp, respectively, with their detailed definition provided in the Methods section. refers to the target diffraction efficiency threshold for . By minimizing the loss function that incorporates the term, we trained 6 diffractive imager models for each design (I, II and III). For each of these models, we set at distinct levels: 0.1%, 0.2%, 0.4%, 0.8%, 1.6% and 3.2%, and trained the respective model to satisfy the specified . Note that all these new diffractive complex field imager models maintain the same physical architecture as the designs illustrated in Fig. 1, and they were trained using the same EMNIST-based complex image dataset. A performance comparison for these models is provided in Fig. 5, where their amplitude and phase average PSNR values were calculated across the test set and shown as a function of their average diffraction efficiency values. Taking the architecture of design III as an example, one of our complex field imager designs achieved an output power efficiency of ~0.2% in both amplitude and phase channels, resulting in average PSNR values of 14.72 ± 1.47 and 16.64 ± 1.03 for the two corresponding channels, respectively. An additional model, optimized with a heightened emphasis on the output power efficiency, demonstrated the capability of performing complex field imaging with >0.8% diffraction efficiency in both the phase and amplitude channels, while achieving average amplitude and phase PSNR values of 13.51 ± 1.32 and 16.74 ± 1.05, respectively. A similar trend was also observed for the other models using designs I and II, where a significant increase in the output diffraction efficiency could be achieved with a modest trade-off in the output image quality. Moreover, a comparative assessment of the three different designs under various output diffraction efficiencies reaffirms the overall performance advantage of design III: it presents remarkable advantages over design I in phase imaging while outperforming design II in amplitude imaging. Overall, Fig. 4 serves as a “designer rule plot”, which offers guidance in selecting suitable diffractive complex field imager models by balancing the phase/amplitude imaging fidelity with output power efficiency according to specific application requirements.
Experimental validation of diffractive complex field imagers
We performed experimental validation of our diffractive complex field imagers using the terahertz part of the spectrum, specifically employing the design II configuration as illustrated in Fig. 1b; we used = 0.75 mm and = 0.8 mm for the phase and amplitude imaging channels, respectively. We used three diffractive layers for our experimental design, each layer containing 120 × 120 learnable diffractive features with a lateral size of ~0.516 (dictated by the resolution of our 3D printer). The axial spacing between any two adjacent layers (including the diffractive layers and the input/output planes) was chosen as ~25.8 (20 mm), resulting in a total axial length of ~103.2 for the entire design. As a proof of concept, we designed two experimental models that use different input phase contrast parameters, and 0.5. These experimental models were trained using a dataset composed of phase-only and amplitude-only objects, which feature randomly generated spatial patterns with binary phase values of {0, } or amplitude values of {0, 1}. In these proof of concept experiments, we did not employ input objects with spatial distributions in both the amplitude and phase channels due to the fabrication challenges of such objects; however, the amplitude-only or phase-only objects used here still share a single common input FOV and are processed by the same diffractive imager. Therefore, this experimental demonstration serves as an effective proof of our all-optical complex field imaging framework, which has never been demonstrated before in prior works.
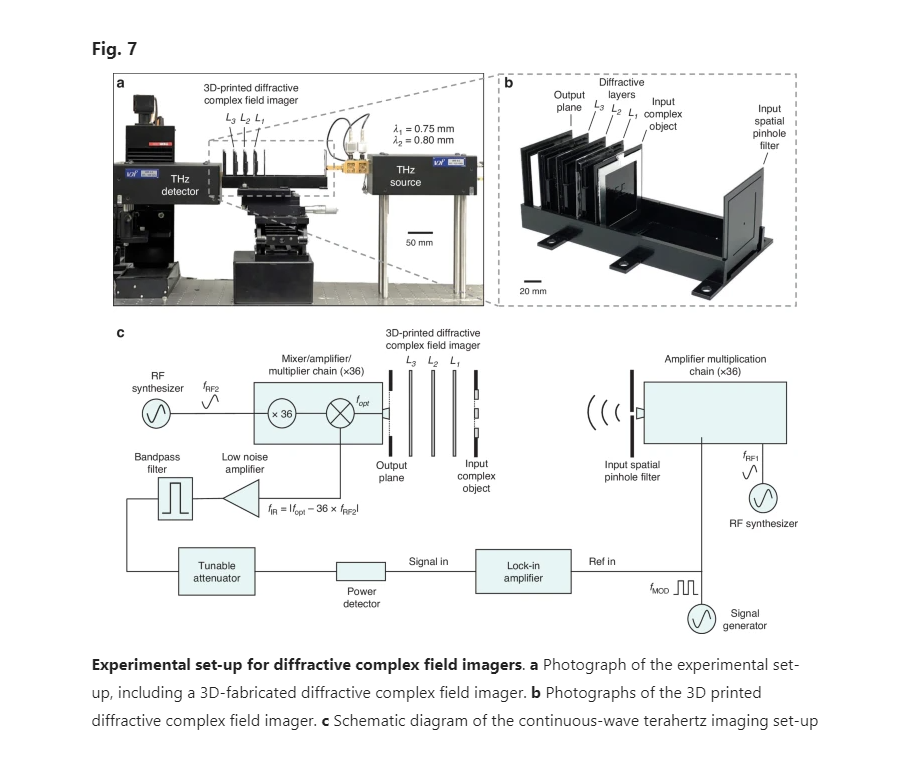
After the training, the resulting layer thickness profiles of the diffractive models with = 1 and 0.5 are visualized in Fig. 6a, d, respectively. These diffractive layers were fabricated using 3D printing, with their corresponding photographs showcased in Fig. 6b, e. Additionally, we constructed phase-only or amplitude-only test objects, which were never seen by the trained diffractive models. The phase-only test objects were fabricated by 3D printing layers with spatially varying height profiles representing the phase distributions, and the amplitude-only objects were created by padding aluminum foils onto 3D-printed flat layers to delineate the amplitude patterns. In our proof-of-concept experiments, these objects were designed to have 5 × 5 pixels, each featuring a size of 4.8 mm (~6.19 ). As shown in Fig. 7b, the printed diffractive layers and input complex objects were assembled using a custom 3D-printed holder to ensure that their relative positions follow our numerical design. In our experiments, we employed a THz source operating at = 0.75 mm and = 0.8 mm, and used a detector to measure the intensity distribution at the output plane, yielding the output amplitude and phase images. The photograph and schematic of our experimental setup are provided in Fig. 7a and c, respectively. Further details related to the experiment are provided in the Methods section.
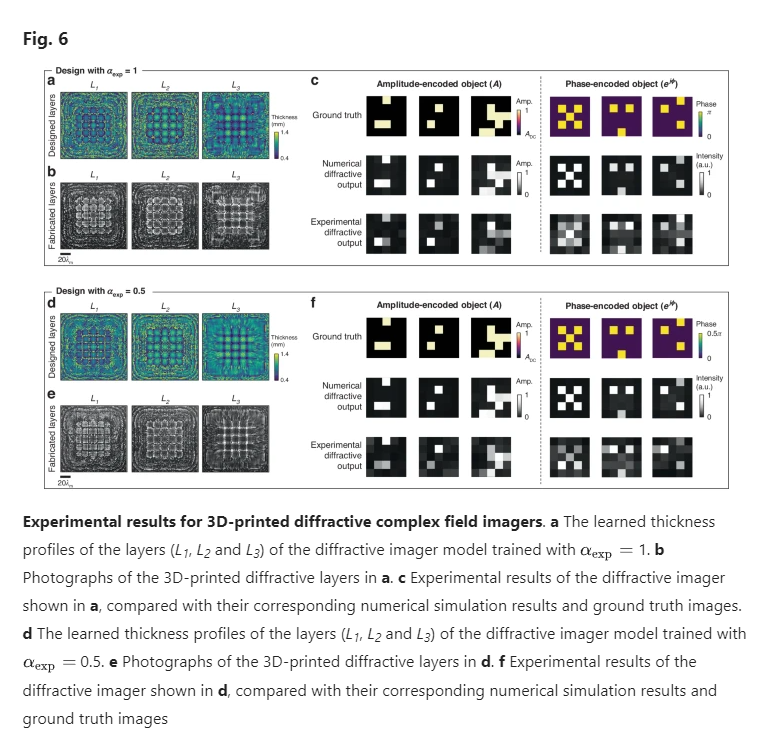
The experimental results for these two models are shown in Fig. 6c, f, where the output amplitude and phase images present a good agreement with their numerically simulated counterparts, also aligning well with the input ground truth images. These experimental results demonstrate the feasibility of our 3D fabricated diffractive complex field imager to accurately image the amplitude and phase distributions of the input objects; these results also represent the first demonstration of all-optical complex field imaging achieved through a single diffractive processor.
Discussion
The numerical analyses and experimental validation presented in our work showcased a compact complex field imager design through deep learning-based optimization of diffractive surfaces. We explored three variants of this design strategy, with comparative analyses indicating that the design employing spatial and wavelength multiplexing (design III) achieves the best balance between the complex field imaging performance and diffraction efficiency, albeit with a minor increase in hardware complexity. Leveraging the all-optical information processing capabilities of multiple spatially engineered diffractive layers, diffractive complex field imagers reconstruct the amplitude and phase distributions of the input complex field in a complete end-to-end manner, without any digital image recovery algorithm, setting it apart from other designs in the existing literature for similar applications. This capability enables direct recording of the amplitude and phase information in a single snapshot using an intensity-only sensor array, which obviates the need for additional computational processing in the back-end, thereby significantly enhancing the frame rate and reducing the latency of the imaging process. Furthermore, our diffractive imager designs feature a remarkably compact form factor, with dimensions of ~100λ in both the axial and lateral directions, offering a substantial volumetric advantage. In contrast, conventional methods based on interferometry and holography often involve relatively bulky optical components and necessitate multiple measurements, leading to optical and mechanical configurations that require a large physical footprint. While some of the recent single-shot complex amplitude imaging efforts using metasurfaces have aimed for greater compactness, they typically require metalenses with large lateral sizes of >1000λ32,37,38. Moreover, achieving a similar FOV (covering several tens of wavelengths) as in our work would require imaging path lengths of thousands of wavelengths.
In our previous research, we developed diffractive processor designs tailored for imaging either amplitude distributions of amplitude-only objects51 or phase distributions of phase-only objects53,59,60. However, these designs would become ineffective for imaging complex objects with independent and non-uniform distributions in the amplitude and phase channels. In this work, we have overcome this limitation by training our diffractive imager designs using complex objects with random combinations of amplitude and phase patterns, thus allowing a single imager device to effectively generalize to complex optical fields with various distributions in the amplitude and phase channels.
The diffractive complex field imager designs that we presented also exhibit certain limitations. Our results revealed residual errors in their targeted operations, particularly manifesting as crosstalk coming from the amplitude channel into the phase channel. This suggests that the actual phase-to-intensity transformation represented by our diffractive imager, while effective, is an approximation with errors that are dependent on the object amplitude distribution. The mitigation approach for this limitation might involve further enhancement of the information processing capacity of our diffractive imagers, which can be achieved through employing a larger number of diffractive layers (forming a deeper diffractive architecture), thus increasing the overall number of diffractive features/neurons that are efficiently utilized64. Additionally, we believe another performance improvement strategy could be to increase the lateral distance between the two output FOVs dedicated to the phase and amplitude channels, thereby allowing the trainable diffractive features to better specialize for the individual tasks of phase/amplitude imaging; this approach, however, would increase the size of the output FOV of the focal plane array and also demand larger diffractive layers.
Moreover, in our experimental results, we observed the emergence of noise patterns within certain regions, which did not exist in our numerical simulations. This discrepancy can be attributed to potential misalignments and fabrication imperfections in the diffractive layers that are assembled. A mitigation strategy could be to perform “vaccination” of these diffractive imager models, which involves modeling these errors as random variables and incorporating them into the physical forward model during the training process42,50,65. This has been proven effective in providing substantial resilience against misalignment errors for diffractive processors, exhibiting a noticeably better match between the numerical and experimental results42,50,65.
Leveraging its unique attributes, our presented complex field imaging system can open up various practical applications across diverse fields. For biomedical applications, it can be seamlessly integrated into endoscopic devices66 and miniature microscopes67,68,69 to enable real-time, non-invasive quantitative imaging of tissues and cells, which might also be useful for, e.g., point-of-care diagnostics with its compactness and efficiency. This might potentially pave the way for their use in intraoperative imaging, providing surgeons with critical, high-resolution insights during a medical procedure70,71. For environmental monitoring, as another example, the presented system may facilitate the development of portable lab-on-a-chip sensors capable of quickly identifying microorganisms and pollutants, streamlining on-site quantitative analysis without delicate and tedious sample preparation steps72,73,74,75. Furthermore, the portability and compactness of these diffractive designs can make them a valuable tool for rapid inspection of materials in industrial settings76,77. Overall, this compact and efficient complex field imager design could be used in various settings, opening new avenues in scientific research and expanding the measurement capabilities for practical, real-world applications.
Materials and methods
Numerical forward model of a diffractive complex field imager
In our numerical implementation, the transmissive layers within the diffractive complex field imager were modeled as thin dielectric optical modulation elements with spatially varying thickness profiles. For the the diffractive layer, the complex-valued transmission coefficient of its the feature at a spatial location was defined depending on the illumination wavelength ( ):
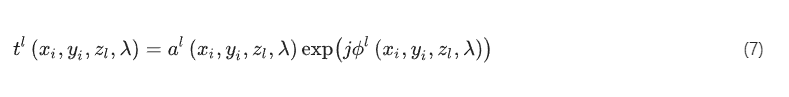
where and denote the amplitude and phase coefficients, respectively. The free-space propagation of complex fields between diffractive layers was modeled through the Rayleigh–Sommerfeld diffraction equation41:
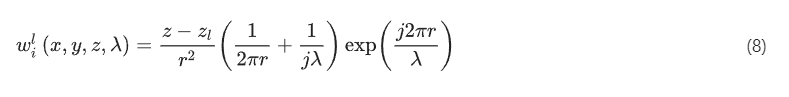
where represents the complex field at the ith diffractive feature of the lth layer at location . and . Based on Eq. (8), can be viewed as a secondary wave generated from the source at . As a result, the optical field modulated by the ith diffractive feature of the lth layer ( ≥ 1, treating the input object plane as the 0th layer), , can be written as:
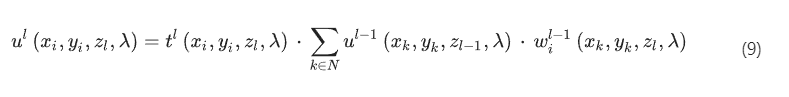
where denotes the number of diffractive features on the (l − 1)th diffractive layer and represents the location of the layer in the z direction parallel to the optical axis. The amplitude and phase components of the complex transmittance of the th feature of diffractive layer , i.e., and in Eq. (7), were defined as a function of the material thickness over the region of that diffractive feature, , as follows:
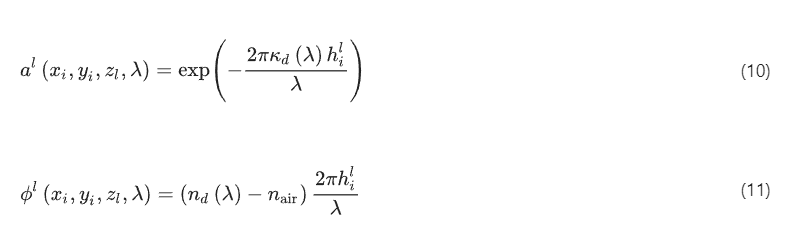
Here the parameters and represent the refractive index and the extinction coefficient of the diffractive layer material, respectively. These parameters correspond to the real and imaginary parts of the complex-valued refractive index, denoted as , such that . We determined the values of and through experimental characterization of the dispersion properties of the diffractive layer materials, and their values are visualized in Supplementary Fig. S6. The trainable thickness values of the diffractive features were limited within the range of [ , ], representing the learnable parameters of our diffractive complex field imagers. For training the diffractive imager models used for numerical analyses, the values of , were selected as 0.2 and 1.2 mm, respectively. For training the diffractive imager models used for experimental validation, the values of , were selected as 0.4 and 1.4 mm, respectively.
Training loss functions and quantification metrics
The total loss function for the training of our diffractive complex field imagers was defined as:
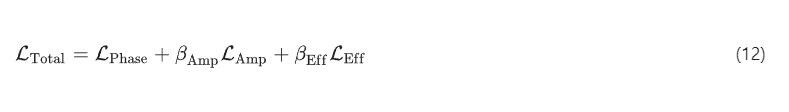
Here, stands for the loss term for the quantitative phase imaging function, and is defined as:
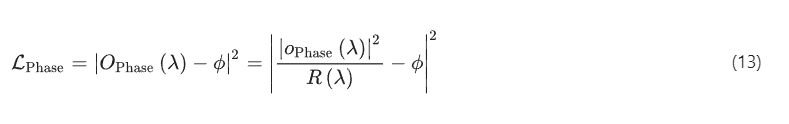
where is the reference signal measured within the reference signal region , which is a frame region surrounding the FOVPhase with a width of one image pixel. represents the loss term for the amplitude imaging function, which is defined as:

where represents the intensity averaging operation across all the spatial pixels of the image. The definition of is provided in Eqs. (4)–(6). In Eqs. (5) and (6), both and were defined using the following Equation:

where represents the total power of the optical field calculated within the output FOV that is either FOVPhase or FOVAmp, i.e., , and represents the total power of the complex field within the input FOV, i.e., .
The hyperparameters, and , in Eq. (12) refer to the weight coefficients associated with the amplitude imaging and output diffraction efficiency penalty-related loss terms, respectively. When training our diffractive imager models shown in Fig. 2a, Supplementary Figs. S1a and S2a, the values of and were set as 3 and 0, respectively, i.e., no diffraction efficiency-related penalty was applied for these models. During the training of the diffractive imager designs exhibiting different output diffraction efficiencies for the analysis in Fig. 4, the values of and were set as 3 and 100, respectively. When training the experimental designs shown in Fig. 6a, d, the values of and were set as 1 and 100, respectively, and were selected as 4%.
For analyzing the imaging performance of our diffractive complex field imagers, we used PSNR as our evaluation metric. The definition of the PSNR value between an image A and an image B is given by: